alcune informazioni sul gioco. | Come si gioca | Regole | Probabilità |

Probabilità vincere nel LOTTO e nel SUPERENALOTTO

PUBBLICITA

M E N U

Qual è la probabilità di azzeccare l' "estratto semplice"? Qual è la probabilità di azzeccare l' "ambo" ?  Qual è la probabilità di azzeccare il "terno" ? Qual è la probabilità di azzeccare la "quaterna"? Qual è la probabilità di azzeccare la "cinquina"? Qual è la probabilità di fare "3"? Qual è la probabilità di fare "4"? Qual è la probabilità di fare "5"? Qual è la probabilità di azzeccare il “5+1”. Qual è la probabilità di fare "6" Al Superenalotto?

Qual è la probabilità di azzeccare l' "estratto semplice"?

Se io gioco un numero, ad esempio il 50, e "spero che esca". 

I casi possibili sono le cinquine non ordinate costruibili con 90 numeri 1, 2, ... 90, cioè

90  5

e i casi favorevoli sono tanti quante le cinquine che contengono il 50.  

Ma queste sono tante quante le quaterne costruibili utilizzando gli 89 numeri rimanenti, cioè

 

89  4

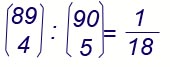
La probabilità richiesta è pertanto:

 

---

Qual è la probabilità di azzeccare l' "ambo" ? 

Se si giocano 2 numeri, ad esempio il 50 e il 75 abbiamo questa situazione statistica:

I casi possibili sono le cinquine non ordinate costruibili coi 90 numeri 1, 2, ... 90, cioè

90  5

 

 

 

e i casi favorevoli sono tanti quante le cinquine che contengono il 50 e il 75. 

Esse sono tante quante le terne costruibili utilizzando gli 88 numeri rimanenti, cioè

88  3

 

 

 

La probabilità richiesta è pertanto

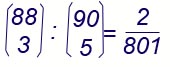vale a dire circa lo 0,0025

 

 

---

Qual è la probabilità di azzeccare il "terno" ?

Se si giocano 3 numeri, ad esempio il 50, il 75 e il 85, quante possibilità si hanno di fare il terno ovvero prenderli tutti e tre?

90  5

I casi possibili sono le cinquine non ordinate costruibili con i nostri soliti 90 numeri 1, 2, ... 90,

ovvero qui a sinistra.

 

e i casi favorevoli sono tanti quante le cinquine che contengono il 50, il 75 e il 85:

87  2

Esse sono tante quante le coppie costruibili utilizzando gli 87 numeri rimanenti,

cioè, come mostra qui a sinistra.

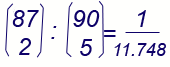
Pertanto la probabilità di fare terno è statistica alla mano di:

vale a dire lo 0,000085. (probabilità del terno)

---

Qual è la probabilità di azzeccare la "quaterna"?

Se si punta alla quaterna e si giocano 4 numeri, ad esempio il 50, il 75, il 85 e 90, qual è la possibilità di vederseli uscire tutti e 4? Ecco la statistica:

I casi possibili sono le cinquine non ordinate realizzabili utilizzando i nostri famosi 90 numeri (1, 2, 3, 4, 5; ecc ecc)

90  5

 

 

 

e i casi favorevoli sono tanti quante le cinquine che contengono il 44, il 55, il 66 e il 77.
che sono tante quanti i numeri rimanenti, ossia sono 86.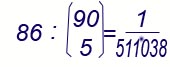

La probabilità richiesta è quindi di:

circa lo 0,0000019. (probabilità di fare cinquina)
 

---

Qual è la probabilità di azzeccare la "cinquina"?

Se si giocano 5 numeri, ad esempio 45, 55, 65, 75, 85 che probabilità ho che esca la cinquina? Ecco la statistica:

90  5

I casi possibili sono le cinquine non ordinate costruibili coi 90 numeri 1, 2, ... 90, cioè

vedi sinistra.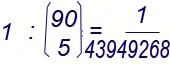

 

Si ha 1 solo caso favorevole.  La probabilità richiesta è pertanto:

ovvero circa: 0,0000000227. (probabilità di fare cinquina al lotto)

Notare come il lotto sia un gioco non equo: in quanto la rendita dalle vincite non eguaglia mai la difficoltà probabilistica (condizione di equità di un gioco), le vincite che fruttano le vincite al lotto sono infatti:

• 11,233 per estratto;
• 55 per estratto determinato;
• 250 per ambo;
• 4.500 per terno;
• 120.000 per quaterna;
• 6.000.000 per cinquina.

SORTE:	PROBABILITA'  MATEMATICA:	COEFFICIENTE DI VINCITA:
Estratto semplice	1/18	11,232
Estratto Determinato	1/90	55
Ambo	2/801 (circa 1/400)	250
Terno	1/11.748	4.500
Quaterna	1/511.038	120.000
Cinquina	1/43.949.268	6.000.000

 

Il gioco del Superenalotto nel Calcolo delle Probabilità

Qual è la probabilità di fare "6" Al Superenalotto?

Io gioco una sestina, ad esempio 10, 20, 30, 40, 50, 60, e "spero che esca".  I casi possibili sono

90  6

le sestine non ordinate costruibili coi 90 numeri 1, 2, ... 90, cioè

 

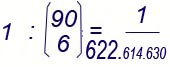
e si ha 1 solo caso favorevole.  La probabilità richiesta è pertanto

ovvero: ... ci siamo capiti.

---

Qual è la probabilità di fare "5"?

Io gioco una sestina, ad esempio 10, 20, 30, 40, 50, 60, e "spero che la nella sestina vincente ci

90  6

siano 5 fra i miei numeri".

I casi possibili sono le sestine non ordinate costruibili coi 90 numeri 1, 2, ... 90, cioè

 

mentre i casi favorevoli sono tanti quante le sestine costruibili utilizzando

5 fra i miei 6 numeri, insieme con 1 degli 84 numeri che non ho giocato.

Esse sono 6 · 84  (6 = numero dei modi in cui, fra i miei 6 numeri, posso sceglierne 5). La probabilità richiesta è pertanto  

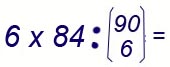0,0000008, probabilità di fare "5"

 

 

---

Qual è la probabilità di fare "4"?

Io gioco una sestina, ad esempio 10, 20, 30, 40, 50, 60, e "spero che la nella sestina vincente ci

90  6

siano 4 fra i miei numeri".

I casi possibili sono le sestine non ordinate costruibili coi 90 numeri 1, 2, ... 90, cioè, a sinistra.

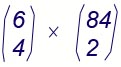
i casi favorevoli sono tanti quante le sestine costruibili utilizzando
4 fra i miei 6 numeri, insieme con 2 degli 84 numeri rimanenti. Esse sono:    .

Infatti

6  4

 

 è il numero dei modi in cui, fra i miei 6 numeri, posso sceglierne 4

84  2

è il numero dei modi in cui, fra gli 84 numeri che non ho giocato, posso sceglierne 2.  

La probabilità richiesta è pertanto: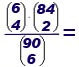 
 

0,0000839, è la probabilità di fare "4" al superenalotto.

 

---

Qual è la probabilità di fare "3"?

Io gioco una sestina, ad esempio 10, 20, 30, 40, 50, 60, e "spero che la nella sestina vincente ci siano 3 fra i miei numeri".

90  6

I casi possibili sono le sestine non ordinate costruibili coi 90 numeri 1, 2, ... 90, cioè 

vedi sinistra.

 

i casi favorevoli sono tanti quante le sestine costruibili utilizzando

3 fra i miei 6 numeri, insieme con 3 degli 84 numeri che non ho giocato.

Esse sono

Infatti

6  3

 

è il numero dei modi in cui, fra i miei 6 numeri, posso sceglierne 3;

 

84  3

 

 è il numero dei modi in cui, fra gli 84 numeri che non ho giocato, posso sceglierne 3). La probabilità richiesta è pertanto

 

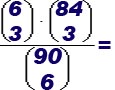
0,003
 

---

 

Andiamo ora a valutare la probabilità di azzeccare il “5+1”.

 

Bene! Il numero dei casi possibili è sempre .

Quanti sono invece i casi favorevoli?

Dunque, ripensiamo a quanto avviene la sera dell’estrazione.

Viene estratta la sestina vincente. Viene poi estratto il numero “jolly”: supponiamo che sia il 58 (il mio anno di nascita è il 1958, ebbene sì). Osserviamo che il numero “jolly” è a tutti gli effetti un settimo numero estratto, quindi è diverso da tutti i numeri della sestina vincente.

I casi favorevoli sono rappresentati da tutte quelle sestine costruibili utilizzando il 58, associato con 5 fra i 6 numeri della sestina vincente.

Ma di sestine siffatte io ne posso costruire, evidentemente, 6 (per scrivere tali sestine, mi basta prendere la sestina vincente e sostituire il primo, oppure il secondo, … , oppure il sesto elemento, col numero 58).

Perciò la probabilità di azzeccare il “5+1” è

ossia esattamente 6 volte la probabilità di azzeccare il “6”. Diciamo quindi meno di 1 su cento milioni.

Non sei convinto di questa risposta? Bravo. Si vede che sei MOLTO attento.

Tu hai stoffa nel calcolo combinatorio, amico.

In effetti, non ti è sfuggito il fatto (da me volutamente taciuto) che qui la prospettiva PSICOLOGICA cambia radicalmente rispetto ai problemi precedenti (valutazione delle probabilità del “6”, del “5”, del “4” e del “3”).

Nei casi precedenti avevamo fissato la nostra attenzione sulla sestina DA NOI GIOCATA; e avevamo ragionato, sostanzialmente, nei termini seguenti:

è come se nell’urna ci fossero, anzichè le palline coi 90 singoli  numeri,  bigliettini, ognuno recante una diversa sestina;

giocando la NOSTRA sestina, è come se noi ci appropriassimo:

di 1 sola sestina fra quelle scritte sui bigliettini, ai fini del “6”;

di  6 84  sestine fra quelle scritte sui bigliettini, ai fini del “5”;…

di   sestine fra quelle scritte sui bigliettini, ai fini del “3”.

Per fissare ancor meglio le idee, potremmo pensare che, giocando la NOSTRA sestina, noi acquisiamo il diritto di “firmare” alcune sestine.

Giocando la nostra sestina”, noi

“firmiamo” 1 sestina fra quelle sui bigliettini, scrivendo anche, accanto alla nostra firma, “se viene pescata questa faccio 6!”

“firmiamo”  6 84  sestine fra quelle sui bigliettini, scrivendo anche, accanto alla nostra firma, “se viene pescata questa faccio 5!”

…

“firmiamo”   sestine fra quelle sui bigl., scrivendo anche, accanto alla nostra firma, “se viene pescata questa faccio 3”.

Se però vogliamo valutare la probabilità di fare “5+1”, ci rendiamo conto che il pensare innanzitutto alla NOSTRA sestina, quella che ci “autorizza a firmare i bigliettini”, non funziona più.

E certo che non può funzionare!

Il fatto è che il numero “jolly” è a tutti gli effetti un settimo numero estratto, quindi dovremmo ragionare in termini di … perdonatemi, non esiste questa parola nella lingua Italiana ma la invento e la utilizzo per brevità … “settimine” anziché sestine.

Oppure potremmo ragionare ancora per sestine, ma in un’ottica diversa.

Fissiamo la nostra attenzione INNANZITUTTO SUI NUMERI CHE VENGONO ESTRATTI, POI, SOLTANTO IN UN SECONDO TEMPO, SULLA NOSTRA GIOCATA.

Il nostro artificio di pensiero è che venga effettuata l’estrazione dei 6+1 numeri, mentre noi nel frattempo siamo chiusi in una cella senza televisore, senza radio e insomma senza possibilità alcuna di comunicare con l’esterno per sapere come è andata l’estrazione.

DOPO l’estrazione, entra il carceriere e ci permette di giocare la nostra sestina.

In queste condizioni, le nostre probabilità di fare “3”, o “4”, o “5”, 0 “6”, o “5+1” evidentemente non cambiano rispetto ad una giocata fatta “nei tempi regolamentari”.

Intanto però l’estrazione è stata già effettuata, ed è come se, ai fini del “5+1”, fossero state selezionate SEI sestine vincenti.

Ne sei convinto? Se, tanto per fare un esempio, sono stati estratti il 2, il 12, il 22, il 32, il 42, il 52, e il 77 come numero jolly,

vincono il “5+1” tutti coloro che hanno giocato una delle sestine

77, 12, 22, 32, 42, 52

2, 77, 22, 32, 42, 52

2, 12, 77, 32, 42, 52

2, 12, 22, 77, 42, 52

2, 12, 22, 32, 77, 52

2, 12, 22, 32, 42, 77

 

E’ come se venisse utilizzata l’urna coi bigliettini ognuno recante una sestina, e venissero firmate 6 di quelle sestine.

Chi ha giocato una di quelle 6 sestine si aggiudica il “5+1”.

Bene! Io però sono in cella, e il carceriere viene a visitarmi perché mi viene data, “nei tempi supplementari”, la possibilità di giocare una sestina.

Questa volta posso immaginare di essere IO, tramite la scelta della MIA sestina, a “pescare” nell’urna contenente i Bigliettini; ai fini del “5+1”, la mia speranza è di beccare proprio uno dei 6 bigliettini firmati.

La probabilità di fare “5+1” è dunque , ossia dobbiamo concludere che la risposta cui eravamo pervenuti senza questa ulteriore riflessione, si rivela comunque corretta. Avevamo proceduto con una certa superficialità, ma ci avevamo azzeccato.

Ora, però, siamo decisamente più convinti della nostra conclusione.

E se volessimo ragionare in termini di “settimine”?

Proviamoci.

A ben guardare, occorre pensare a settimine che non sono né “completamente ordinate” né “completamente non ordinate”.

Le settimine a cui dobbiamo pensare sono composte da: 6 elementi di cui non conta l’ordine ma solo l’individualità; più un settimo elemento (il “jolly”), di cui conta invece il fatto che è proprio il settimo numero estratto.

Dunque, le settimine POSSIBILI, quante sono?

Quanti sono i possibili esiti dell’estrazione dei fatidici 6+1 numeri il sabato sera?

Sono tanti quanti sono i modi di scegliere (non importa l’ordine) 6 numeri fra i 90 disponibili, PIU’ un settimo numero fra gli 84 rimanenti.

E questa doppia scelta può essere effettuata in modi. Altrettante sono dunque le settimine possibili:

E le settimine a me FAVOREVOLI in vista del “5+1”, quando scelgo 6 numeri e li gioco?

Dunque, io non sono più in carcere, sono un uomo libero; è sabato pomeriggio e vado in ricevitoria a giocare la mia sestina, diciamo la solita 10, 20, 30, 40, 50, 60 a cui sono affezionato.

Nell’ottica del “5+1”, allora, io vado a “firmare” un bel po’ di settimine fra le settimine possibili.

Vado a “firmare” ad esempio la settimina 60, 40, 10, 30, 20, 71, 50:

se esce questa settimina, ossia se i sette numeri estratti sono, in ordine di estrazione, 60, 40, 10, 30, 20, 71, 50,

io faccio “5 + 1”.

Anche se esce 30, 36, 20, 10, 40, 60, 50 io faccio “5+1”.

Anche se esce 60, 50, 40, 30, 20, 48, 10 io faccio “5+1”.

Insomma, con la mia giocata, io faccio “5+1” se esce una settimina composta da:

6 termini iniziali (quelli di cui non importa l’ordine”) costituiti da 5 fra i 6 numeri da me scelti, insieme con un numero che sta fra gli 84 numeri da me NON scelti; e da un numero finale, coincidente col numero rimanente della mia sestina.

Ma di sestine siffatte io ne posso costruire (e quindi “firmare”)

Pertanto la probabilità di fare “5+1” è data dal numero

 che, guarda caso, coincide con la probabilità trovata attraverso l’altro procedimento.

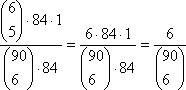
In quanto all’equità o iniquità del Superenalotto, la valutazione è un po’ più elaborata rispetto a quella fatta per il Lotto, in quanto il premio in caso di vincita non si ottiene, come nel caso del Lotto, moltiplicando la cifra impegnata per un dato fattore (dipendente dal tipo di combinazione giocata), ma invece il frutto della ripartizione di un “monte-premi” variabile di settimana in settimana; fra i vari giocatori che hanno azzeccato le varie combinazioni.

Lo studente, a questo punto, potrà facilmente approfondire la questione pervenendo alla stessa conclusione precedente:

Lotto | Gioco d'azzardo | previsioni enalotto | previsioni gratis lotto |