Due parole sulla statistica matematica applicabile a lotto/enalotto

Statistica Permutazioni Dismutazioni Disposizioni senza ripetizioni Disposizioni con ripetizioni Combinazioni senza ripetizioni  Combinazioni con ripetizioni PUBBLICITA

La Statistica:

La Statistica è una scienza di derivazione matematica che si occupa di studiare e descrivere la realtà fenomenica nei suoi aspetti di rilevazione numerica. Deriva pertanto le sue regole e le sue valutazioni qualitative attraverso l'analisi di rilevamenti quantitativi opportunamente selezionati.

La metodologia statistica viene suddivisa tradizionalmente in due branche, strettamente collegate:

statistica descrittiva
statistica inferenziale
La prima ha ad oggetto indicatori statistici (indicatori di posizione, di variazione, di concentrazione, di correlazione, ecc.) per riassumere con pochi numeri (media, varianza, ecc.) realtà anche complesse.

La statistica inferenziale ha come obiettivo di fare affermazioni valide anche per fenomeni che non sono stati osservati, generalizzando i risultati a partire dal dato empirico; studia inoltre la verifica di ipotesi. Per fare ciò ricorre agli strumenti della teoria della probabilità.

Calcolo Combinatorio:

Il calcolo combinatorio è il termine che denota tradizionalmente la branca della matematica che studia i modi per raggruppare e/o ordinare secondo date regole gli elementi di un insieme finito di oggetti. Il calcolo combinatorio si interessa soprattutto di contare tali modi, ovvero le configurazioni e solitamente risponde a domande quali "Quanti sono...", "In quanti modi...", "Quante possibili combinazioni..." ecc.

Più formalmente, dato un insieme S di n oggetti si vuole contare le configurazioni che possono assumere k oggetti tratti da questo insieme. Prima di affrontare un problema combinatorio bisogna capire due fatti importanti:

PUBBLICITA

Se l'ordinamento è importante, ovvero se due configurazioni sono le stesse a meno di un riordinamento ((x,y,z) è uguale a (z,x,y)?)
Se si possono avere più ripetizioni di uno stesso oggetto, ovvero se uno stesso oggetto dell'insieme può o meno essere riusato più volte all'interno di una stessa configurazione.  torna SU.

Permutazioni:

Una permutazione di un insieme di oggetti è una presentazione ordinata, cioè una sequenza, dei suoi elementi nella quale ogni oggetto viene presentato una ed una sola volta. Per contare quante siano le permutazioni di un insieme con n oggetti, si osservi che il primo elemento della configurazione può essere scelto in n modi diversi, il secondo in (n - 1), il terzo in (n - 2) e così via sino all'ultimo che potrà essere preso in un solo modo essendo l'ultimo rimasto. Dunque, indicando con Pn il numero delle possibili permutazioni, si ottiene che esse sono esattamente n! (n fattoriale):

Ad esempio le permutazioni degli elementi dell'insieme {a,b,c} sono 3! = 6: abc, acb, bac, bca, cab, cba.

torna SU.

Dismutazioni senza rietizioni:

Una disposizione semplice di lunghezza k di elementi di un insieme S di n oggetti, con k < n, è una presentazione ordinata di k elementi di S nella quale non si possono avere ripetizioni di uno stesso oggetto. Per avere il numero di queste configurazioni si considera che il primo componente di una tale sequenza può essere scelto in n modi diversi, il secondo in (n - 1) e così via sino al k - esimo che può essere scelto in (n - k + 1) modi diversi. Pertanto il numero di disposizioni semplici di k oggetti estratti da un insieme di n oggetti è dato dal prodotto:

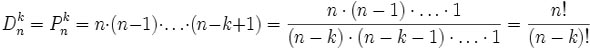
Ad esempio le disposizioni semplici di lunghezza 2 degli elementi dell'insieme {1,2,3,4,5} sono : 12, 13, 14, 15, 21, 23, 24, 25, 31, 32, 34, 35, 41, 42, 43, 45, 51, 52, 53, 54.

Si osserva che le permutazioni sono casi particolari delle disposizioni semplici: le permutazioni di un insieme di n oggetti sono le disposizioni semplici di tali oggetti di lunghezza n. In effetti per il loro numero:

torna SU.

Disposizioni con ripetizioni:

Una presentazione ordinata di elementi di un insieme nella quale si possono avere ripetizioni di uno stesso elemento si dice disposizione con ripetizioni. Cerchiamo il numero delle possibili sequenze di k oggetti che riproducono gli elementi di un insieme di n oggetti ognuno dei quali può essere preso più volte. Si hanno n possibilità per scegliere il primo componente, n per il secondo ed altrettante per il terzo e così via sino al k - esimo che completa la configurazione. Il numero cercato è pertanto:

Ad esempio le disposizioni con ripetizione di lunghezza 2 degli elementi di {1,2,3,4,5} sono:

52 = 25: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43, 44, 45, 51, 52, 53, 54, 55.

torna SU.

Combinazioni senza ripetizioni:

Si chiama combinazione semplice una presentazione di elementi di un insieme nella quale non ha importanza l'ordine dei componenti e non si può ripetere lo stesso elemento più volte. La collezione delle combinazioni di k elementi estratti da un insieme S di n oggetti distinti si può considerare ottenuta dalla collezione delle disposizioni semplici di lunghezza k degli elementi di S ripartendo tali sequenze nelle classi delle sequenze che presentano lo stesso sottoinsieme di S e scegliendo una sola sequenza da ciascuna di queste classi. Si osserva che ciascuna delle suddette classi di sequenza di lunghezza k contiene k! sequenze, in quanto accanto a una sequenza σ si hanno tutte e sole quelle ottenibili permutando i componenti della σ. Quindi il numero delle combinazioni semplici di n elementi di lunghezza k si ottiene dividendo per k! il numero delle disposizioni semplici di n elementi di lunghezza k:

Di solito tra le diverse disposizioni semplici di una classe si sceglie come combinazione rappresentativa la sequenza nella quale i componenti compaiono in ordine crescente (tutti gli insiemi finiti possono avere gli elementi ordinati totalmente, ovvero associati biunivocamente ai primi interi positivi).

Ad esempio le combinazioni semplici di lunghezza 4 degli elementi di {1,2,3,4,5,6} sono :

1234, 1235, 1236, 1245, 1246, 1256, 1345, 1346, 1356, 1456, 2345, 2346, 2356, 2456, 3456.

torna SU.

Combinazioni con ripetizioni:

Quando l'ordine non è importante ma è possibile avere componenti ripetute si parla di combinazioni con ripetizione. Nelle combinazioni con ripetizione di lunghezza k ogni elemento può essere ripetuto fino a k volte. Pensiamo in particolare alle combinazioni con ripetizione di lunghezza k dell'insieme dei primi n interi positivi e più precisamente alle sequenze non decrescenti di lunghezza k di interi in {1,2,...,n}. Consideriamo una di queste sequenze e associamole la sequenza 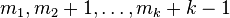. Si constata che la nuova sequenza è strettamente crescente, non presenta ripetizioni e quindi individua una combinazione semplice di lunghezza k degli interi in {1, 2, ..., n+k-1). La precedente associazione pone in corrispondenza biunivoca le combinazioni con ripetizioni di lunghezza k degli elementi di {1, 2, ..., n} con le combinazioni semplici di lunghezza k degli interi in {1, 2, ..., n+k-1). Quindi il numero delle combinazioni con ripetizioni di lunghezza k dei primi n interi positivi coincide con il numero delle combinazioni semplici di lunghezza k dei primi n+k-1 interi positivi:

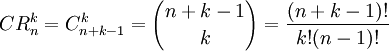
Ad esempio le combinazioni con ripetizione di lunghezza 2 degli elementi di {1,2,3,4,5} sono : 11, 12, 13, 14, 15, 22, 23, 24, 25, 33, 34, 35, 44, 45, 55.

torna SU.

fonte: http://it.wikipedia.org/wiki/Calcolo_combinatorio ; licenza GNU

vuoi commentare questo previsione o comunicarci un tuo sistema? contattaci: clicca qui